Rutherford’s Alpha( ) Particle Scattering
) Particle Scattering
- The entire charge and almost entire mass of the atom is concentrated in a single core of the atom is called nucleus and is surrounded by Negatively(-) charged electron clouds.
- The
particle and gold nuclei are so small that they may be treated as a point mass and point charge.
- The nucleus is considered so heavy that its motion during the scattering process may be neglected.
- The scattering is due to the coulombs force of repulsion between the
particle and the Gold Nucleus.
- Each
particle suffers a single deflection.
- The
particles do not penetrate the nuclear region. So strong nuclear forces are not involved in their interaction.
Derivation Of Rutherford’s Scattering Formula
Let an particle is moving along PO apparatus and the relatively heavy nucleus stationary at it. Since both are Positively(+) charged so there is a force of repulsion between them. As
particle gets closer to the nucleus the repulsive force highly increases and the
particle follows a hyperbolic path. The asymptotes and po and p’o give the initial and final reflection of
particle.
Let the perpendicular drawn from the nucleus to PO is NM and is the shortest distance between the nucleus and initial direction of 𝞪- particle which is known as impact parameters(b).
Let
- Z be the atomic no. of the element That scattered
particle.
- Ze be the charge of the nucleus.
- θ, be the scattering angle or angle of deviation of
particle.
- As the
particle moves its momentum changes from
to
i.e
using sine law in
Now From Equation (1)
where t = ,
t = ;
From Eq (2)
As the radius joining the
— particle and the nucleus is along the direction of the force. So there is no torque acting on the
— particle.
The angular momentum remain content
[ L=R *P =Rmv=bmv ]
putting this in EQ (3)
But
putting this EQ (4)
where k=K.E
This is the relation between scatting angle and impact parameter.
In the actual experiment, a large number of particle are incident various impact parameter all around the (Au) Gold nucleus.
According to EQ(5), the particle that approaches the nucleus with impact parameter “b” will be scattered at an angle “
“
Particle approaching with the smallest value of “b” (i.e
b) will be scattered through large angle (i.e
)
The Area of cross-section of radius it.e is called scattering cross-section i.e
Consider a thin gold foil of thickness “t” and cross – section “A”. Suppose it contains ‘n’ number of atoms per unit volume, then the volume of the foil is “At”.
Then the number of target nuclei in the foil is “nAt”. We assume that the foil is so thin that particle suffers single deflection i.e , one
particle is scattered by one gold nucleus.
Since one nucleus has cross – section .
So area of cross – section of “nAt” nuclei = .
Let ‘N’ be the total number of particle and “
” be the Number of
particle being scattered by an angle
Then the fraction of incident
particles scattered by an angle
is
as
——————————————-
as we know from Eq(5)
——————————————-
But a particle detector measures the Number of df i.e,
The scattered particle strikes the screen placed at a distance “r” from the foil. The area ds is struck by these particles is the area of the ring of radius rsin
and thickness “
” is
Then
Where N(0) represents the number of particle per unit area striking the screen. This is the expression for Rutherford’s Scattering formula.
Experimental Verification of Rutherford’s Alpha particle scattering Formula
The Theory of Rutherford’s Particle scattering was verified by a series of experiments conducted by Gaiger and Marsden in 1913.
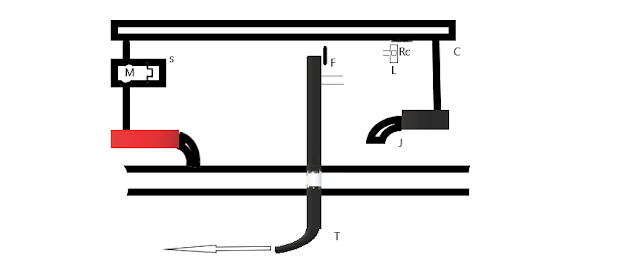
The experimental arrangement consists of an Airtight chamber (c) which can be evacuated by tube (T). The chamber is capable of rotating inside the jacket ( J ) about a vertical axis. Radon is taken as the Radioactive source Rc of particles Which is placed inside a Radioactive cell (L).
After coming out of the narrow opening lead cavity the particle strikes a thin foil (F) (Gold, Silver, Platinum ).The foil is placed at the centre of the chamber (c).The scattered
particles are viewed through low Power Microscope (M) which is provided with a fluorescent screen. As the chamber rotates about a central axis the microscope rotates along with it but the cavity (L) and foil(f) remain fixed with the tube. The
particles striking on the foil get scattered in a different direction. The number of
particles scattering along different direction can be recorded by observing the scintillations on the fluorescent screen.
The Following Results Obtained From The Above Experiment:-
- Most of the
particle either passed straight through the metal foil or suffered only small deflection. This could be explained by Thomson’s Atomic Model.
- A few
particle were deflected through angle where were less than 90 degree (
) and a very few
particle were deflected through an angle greater than 90 degree (
). Sometimes a particle was found to be deflected through 180 degree(
) . These large angle scattering could not be explained by Thomson’s Atomic Model
- If
is the scattering angle and N is the number of Particles available in that direction then it is found that
4.If “t” is the thickness of the foil and N is the number of
5. This experiment also verified that Number of particles “N” scattered along scattering angle
is directly proportional to (
) square of the Atomic Number of the foil atom i.e
Size of the nucleus from alpha( ) particles scattering:-
) particles scattering:-
Initial Kinetic Energy of particle =
Initial Potential Energy of particle = 0
Final Kinetic Energy of particle = 0
Final Kinetic Energy of particle =
From energy conservation law,
Initial Total Energy = Final Total Energy
the charge of particle = 2e
the charge of nucleus = Ze
by putting the value of m,v and Z for given experiment we can find the radius of given nucleus.
Q. In an experiment velocity of particle is
m/s is bombarded upon Gold Z= 79,
Mass of particle M=
, Then what is the radius of the nucleus?
 Failure of Rutherford’s scattering formula
Failure of Rutherford’s scattering formula
2. According to Rutherford’s mode electron can revolve in any orbit, So it must emit continuous radiation of all frequencies but elements emit spectral lines of only definite frequency.